Baldur Sigurðsson

I specialize in the topological study of singularity theory over the complex numbers, especially the relationship between surface singularities and low dimensional topology. Currently, I am interested in using tropical methods, extending methods which use Newton diagrams, studying the Lipschitz geometry of nonisolated singularities, as well as extending tête-à-tête methods to higher dimensions. I also do a bit of programming, mostly to compute examples.

Status

Current

I am currently a María Zambrano postdoc at Universidad Complutense Madrid.

Former

• I finished a BS degree at The University of Iceland (HÍ) in 2008,
• an MS degree at Eötvös Loránd Tudományegyetem (ELTE) in 2010,
• and a PhD at CEU under the supervision of András Némethi in December 2015.
• I also worked on normal surface singularities as part of the low dimensional topology team at the Alfréd Rényi Institute of Mathematics. until February 2016.
• From then, and until November 2018, I was a postdoc working with the singularity theory and algebraic geometry group at Basque Center for Applied Mathematics BCAM in Bilbao.
• I was a postdoc 2018-2020 at the math department of UNAM in Cuernavaca, Mexico.
• I was a Simons postdoc 2021-2022 at the Institute of Mathematics, Vietnam Academy of Science and Technology, Hanoi.

CV

Curriculum vitae.

Docencia

Curvas Algebraicas otoño 2022.

Curvas Algebraicas otoño 2023.

Written content

Preprints

Joint with Pablo Portilla Cuadrado, The total spine of the Milnor fibration of a plane curve singularity, 2023.

Joint with András Némethi, Local Newton nondegenerate Weil divisors in toric varieties, 2021.

Articles

On ideal filtrations for Newton nondegenerate surface singularities. In Singularities and their interaction with geometry and low dimensional topology, Trends Math., pages 13–32. Birkhäuser/Springer, Cham, 2021.

Joint with Pablo Portilla Cuadrado, Mixed tête-à-tête twists as monodromies associated with holomorphic function germs, https://doi.org/10.1007/s10711-020-00533-7 2020.

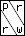The boundary of the Milnor fiber of the singularity 𝑓(𝑥,𝑦)+𝑧𝑔(𝑥,𝑦)=0. European Journal of Mathematics (2020) doi:10.1007/s40879-019-00393-w

Joint with András Némethi, The geometric genus of hypersurface singularities, J. Eur. Math. Soc. (JEMS) 18, No. 4, 825-851 (2016).

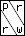The Milnor fiber of the singularity f(x,y) + zg(x,y) = 0. Rev Mat Complut (2016) 29: 225. doi:10.1007/s13163-015-0179-5.

Presentations

The geometric genus of hypersurfaces, presented on the 13th International Workshop on Real and Complex Singularities Celebrating the 60th birthday of María del Carmen Romero Fuster July 27th - August 1st 2014.

Thesis

The geometric genus and the Seiberg-Witten invariant of Newton nondegenerate surface singularities.

Slides presented during the defense.

Code

A program for calculating invariants related to lattice cohomology.

A collection of functions related to numerical invariants of surface singularities written in PARI/GP. Includes an implementation of Oka's algorithm. Be warned that the function that calculates the Turaev torsion is flaky. I'll have to redo that whole thing, but until then, don't take it as absolute truth. In particular, the Seiberg-Witten invariant may be incorrect.

A collection of small projects.

An implementation of plumbing graphs in sage. This is work in progress, but it will hopefully get accepted into the sage project soon. Some functionality is still lacking, and there are probably some errors in there, since it hasn't been tested much. This is where you come in!

Notes

Here are some notes on various issues. I'm mostly collecting them here for myself, but maybe they are of help to others.

Contact